Alumni Gazette
 Bird No. 74 (detail, left), is based on a parallelogram. Beetle No. 91 (detail, right), is based on a rhombus. (Photo: All M.C. Escher works © 2016 The M.C. Escher Company—the Netherlands. All rights reserved. Used by permission. www.mcescher.com)
Bird No. 74 (detail, left), is based on a parallelogram. Beetle No. 91 (detail, right), is based on a rhombus. (Photo: All M.C. Escher works © 2016 The M.C. Escher Company—the Netherlands. All rights reserved. Used by permission. www.mcescher.com)Schattschneider offers several tessellation “recipes,” similar to those that Escher discovered after much investigation. In general, tessellations are created either by taking a simple shape and modifying it through geometric translation (moving corresponding endpoints of opposite sides by the same distance and in the same direction); or by modifying a shape through translation and reflection (the creation of a mirror image).
Follow these recipes to create your own tessellations, manually or with software programs such as The Geometer’s Sketchpad, GeoGebra, Cabri, or TesselManaic.
Using translation

Parallelogram
- Replace two adjacent sides (a and b above) with any series of lines or curves that connect the endpoints of the sides.
- Translate the new lines or curves to their opposite sides.

Par-hexagon
- Replace three adjacent sides (a, b, and c above) with curves that connect the endpoints of the sides.
- Translate the new lines or curves to their opposite sides.
- To tile the plane, translate the tile so that opposite edges match.
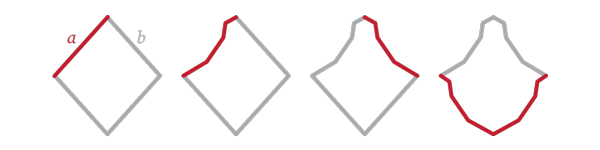
Using reflection and translation
- Begin with a rhombus to create a tile with reflection symmetry.
- Replace one side of the rhombus with a curve that connects the endpoints of the side (side a above).
- Reflect that curve in a diagonal of the rhombus that meets one of those endpoints (reflect to replace side b above).
- Translate the two curves to their opposite sides.
- To tile the plane, simply translate the tile so that opposite edges match.

